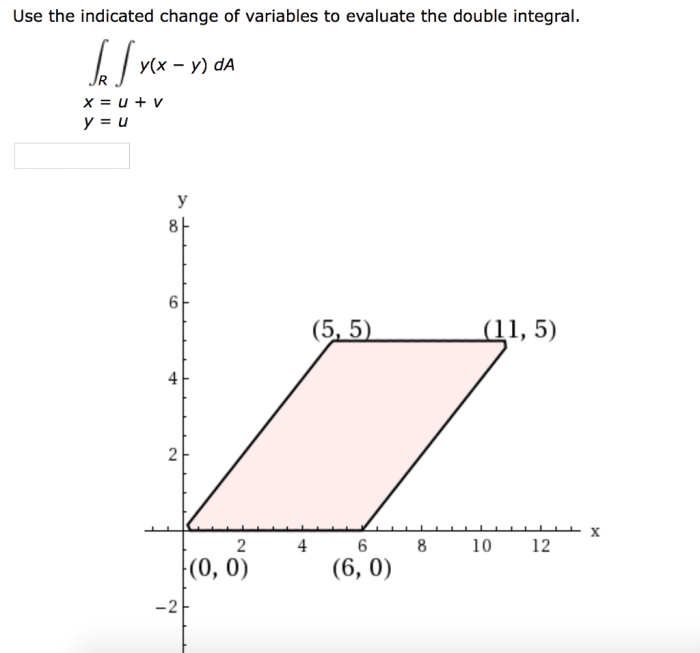
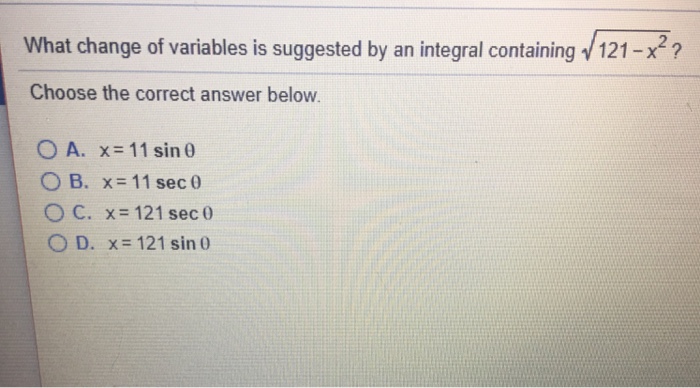
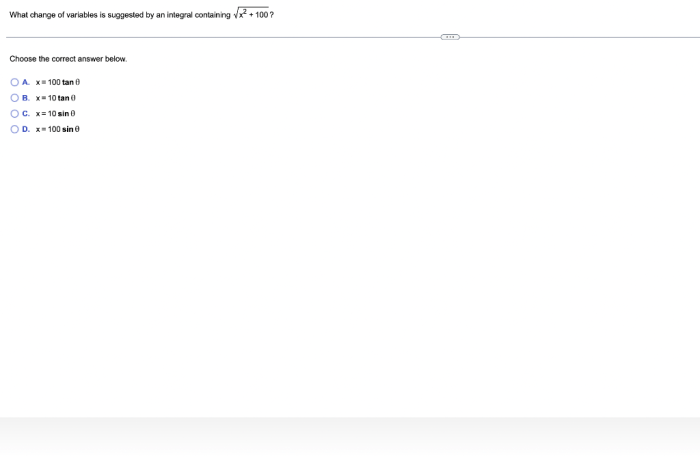
What change of variables is suggested by an integral containing? This question lies at the heart of integral calculus, a branch of mathematics that deals with the computation of integrals. Integrals are used to find areas, volumes, and other quantities that arise in various applications.
In this article, we will explore the different techniques for changing variables in integrals and discuss how to identify the most appropriate transformation for a given integral.
One of the most common variable transformation techniques is u-substitution. This technique involves substituting a new variable, u, for a term in the integrand that can be differentiated to give the original integrand. For example, if we have an integral of the form ∫f(x)dx, we can use u-substitution to transform it into ∫f(u)du, where u = g(x) and du = g'(x)dx.
Variable Transformation Techniques
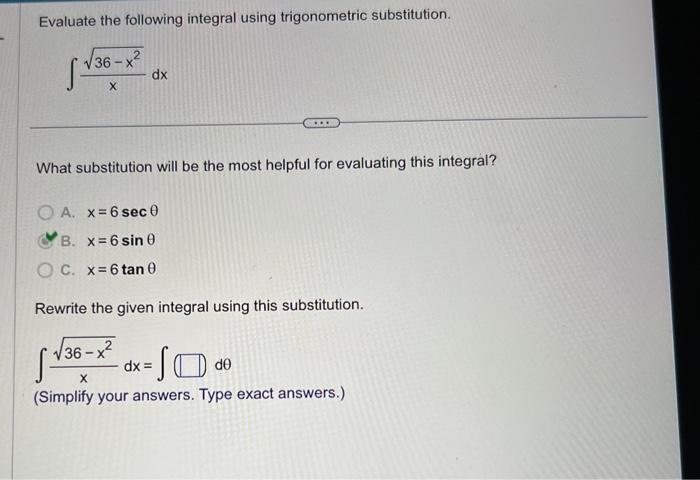
Variable transformation is a powerful technique in integral calculus that allows us to simplify integrals by changing the variable of integration.
There are several common variable transformation techniques, including:
- u-substitution: This technique involves substituting a new variable ufor a function of the original variable x.
- Trigonometric substitution: This technique is used to evaluate integrals involving trigonometric functions.
- Hyperbolic substitution: This technique is similar to trigonometric substitution, but it is used to evaluate integrals involving hyperbolic functions.
Each of these techniques can be applied to simplify integrals in a variety of situations. For example, u-substitution can be used to evaluate integrals of the form ∫f(g(x))g'(x)dx, while trigonometric substitution can be used to evaluate integrals of the form ∫sin nxcos mxdx.
Identifying Suitable Transformations
The key to successful variable transformation is choosing the right transformation for the given integral. The following criteria can help you select the most appropriate transformation:
- The form of the integrand: The form of the integrand can often suggest the appropriate transformation. For example, if the integrand contains a trigonometric function, then trigonometric substitution may be a good choice.
- The presence of trigonometric or hyperbolic functions: If the integrand contains trigonometric or hyperbolic functions, then trigonometric or hyperbolic substitution may be necessary.
For example, consider the integral ∫sin 2xcos 3xdx. The presence of the trigonometric functions suggests that trigonometric substitution may be a good choice.
Integration by Parts
Integration by parts is another technique that can be used to simplify integrals. The integration by parts formula is given by:
∫udv = uv
∫vdu
where uand vare differentiable functions of x.
Integration by parts can be used to transform integrals into more manageable forms. For example, consider the integral ∫xsin x dx. Using integration by parts with u= x and dv= sin x dx, we get:
∫xsin x dx = x(-cos x)
- ∫(-cos x)dx =
- xcos x + sin x + C
Partial Fraction Decomposition, What change of variables is suggested by an integral containing
Partial fraction decomposition is a technique that can be used to simplify integrals of rational functions. A rational function is a function that can be expressed as the quotient of two polynomials.
Partial fraction decomposition involves expressing the rational function as a sum of simpler fractions, which can then be integrated more easily. For example, consider the integral ∫(x^2 + 1)/(x^2 – 1) dx. Using partial fraction decomposition, we can express the integrand as:
(x^2 + 1)/(x^2
- 1) = 1 + 2/(x
- 1)
- 2/(x + 1)
We can then integrate each of these terms separately to get:
∫(x^2 + 1)/(x^2
- 1) dx = x + 2ln|x
- 1|
- 2ln|x + 1| + C
Frequently Asked Questions: What Change Of Variables Is Suggested By An Integral Containing
What is the purpose of changing variables in integrals?
Changing variables in integrals allows us to simplify integrals and make them easier to solve.
What are the different techniques for changing variables in integrals?
The most common variable transformation techniques are u-substitution, trigonometric substitution, and hyperbolic substitution.
How do I identify the most appropriate transformation for a given integral?
The most appropriate transformation for a given integral can be identified by examining the form of the integrand and the presence of trigonometric or hyperbolic functions.